Basic Tutorial III: Functional Workflow¶

Introduction¶

AutoRA (Automated Research Assistant) is an open-source framework designed to automate various stages of empirical research, including model discovery, experimental design, and data collection.

This notebook is the third of four notebooks within the basic tutorials of autora. We suggest that you go through these notebooks in order as each builds upon the last. However, each notebook is self-contained and so there is no need to run the content of the last notebook for your current notebook.

These notebooks provide a comprehensive introduction to the capabilities of autora. It demonstrates the fundamental components of autora, and how they can be combined to facilitate automated (closed-loop) empirical research through synthetic experiments.

How to use this notebook You can progress through the notebook section by section or directly navigate to specific sections. If you choose the latter, it is recommended to execute all cells in the notebook initially, allowing you to easily rerun the cells in each section later without issues.

Tutorial Setup¶

We will here import some standard python packages, set seeds for replicability, and define a plotting function.

In [ ]:

#### Installation ####
!pip install -q "autora[theorist-bms]"
!pip install -q "autora[experiment-runner-synthetic-abstract-equation]"

#### Import modules ####
from typing import Optional
import numpy as np
import pandas as pd
import sympy as sp
import torch
import matplotlib.pyplot as plt

from autora.state import StandardState

#### Set seeds ####
np.random.seed(42)
torch.manual_seed(42)

#### Define plot function ####
def plot_from_state(s: StandardState, expr: str):    
    
    """
    Plots the data, the ground truth model, and the current predicted model
    """
    
    #Determine labels and variables
    model_label = f"Model: {s.models[-1]}" if hasattr(s.models[-1],'repr') else "Model"
    experiment_data = s.experiment_data.sort_values(by=["x"])
    ground_x = np.linspace(s.variables.independent_variables[0].value_range[0],s.variables.independent_variables[0].value_range[1],100)
    
    #Determine predicted ground truth
    equation = sp.simplify(expr)
    ground_predicted_y = [equation.evalf(subs={'x':x}) for x in ground_x]
    model_predicted_y = s.models[-1].predict(ground_x.reshape(-1, 1))

    #Plot the data and models
    f = plt.figure(figsize=(4,3))
    plt.plot(experiment_data["x"], experiment_data["y"], 'o', label = None)
    plt.plot(ground_x, model_predicted_y, alpha=.8, label=model_label)
    plt.plot(ground_x, ground_predicted_y, alpha=.8,  label=f'Ground Truth: {expr}')
    plt.xlabel('x')
    plt.ylabel('y')
    plt.legend()
    plt.show()

#### Installation #### !pip install -q "autora[theorist-bms]" !pip install -q "autora[experiment-runner-synthetic-abstract-equation]" #### Import modules #### from typing import Optional import numpy as np import pandas as pd import sympy as sp import torch import matplotlib.pyplot as plt from autora.state import StandardState #### Set seeds #### np.random.seed(42) torch.manual_seed(42) #### Define plot function #### def plot_from_state(s: StandardState, expr: str): """ Plots the data, the ground truth model, and the current predicted model """ #Determine labels and variables model_label = f"Model: {s.models[-1]}" if hasattr(s.models[-1],'repr') else "Model" experiment_data = s.experiment_data.sort_values(by=["x"]) ground_x = np.linspace(s.variables.independent_variables[0].value_range[0],s.variables.independent_variables[0].value_range[1],100) #Determine predicted ground truth equation = sp.simplify(expr) ground_predicted_y = [equation.evalf(subs={'x':x}) for x in ground_x] model_predicted_y = s.models[-1].predict(ground_x.reshape(-1, 1)) #Plot the data and models f = plt.figure(figsize=(4,3)) plt.plot(experiment_data["x"], experiment_data["y"], 'o', label = None) plt.plot(ground_x, model_predicted_y, alpha=.8, label=model_label) plt.plot(ground_x, ground_predicted_y, alpha=.8, label=f'Ground Truth: {expr}') plt.xlabel('x') plt.ylabel('y') plt.legend() plt.show()

WARNING: typer 0.12.3 does not provide the extra 'all'
WARNING: typer 0.12.3 does not provide the extra 'all'

States¶

Using the functions and objects in autora.state, we can build flexible pipelines and cycles which operate on state objects. State objects represent data from an experiment, like the conditions, observed experiment data and models. The State also includes rules on how to update those data if new data are provided using the "Delta mechanism". This state can be acted upon by experimentalists, experiment runners, and theorists.

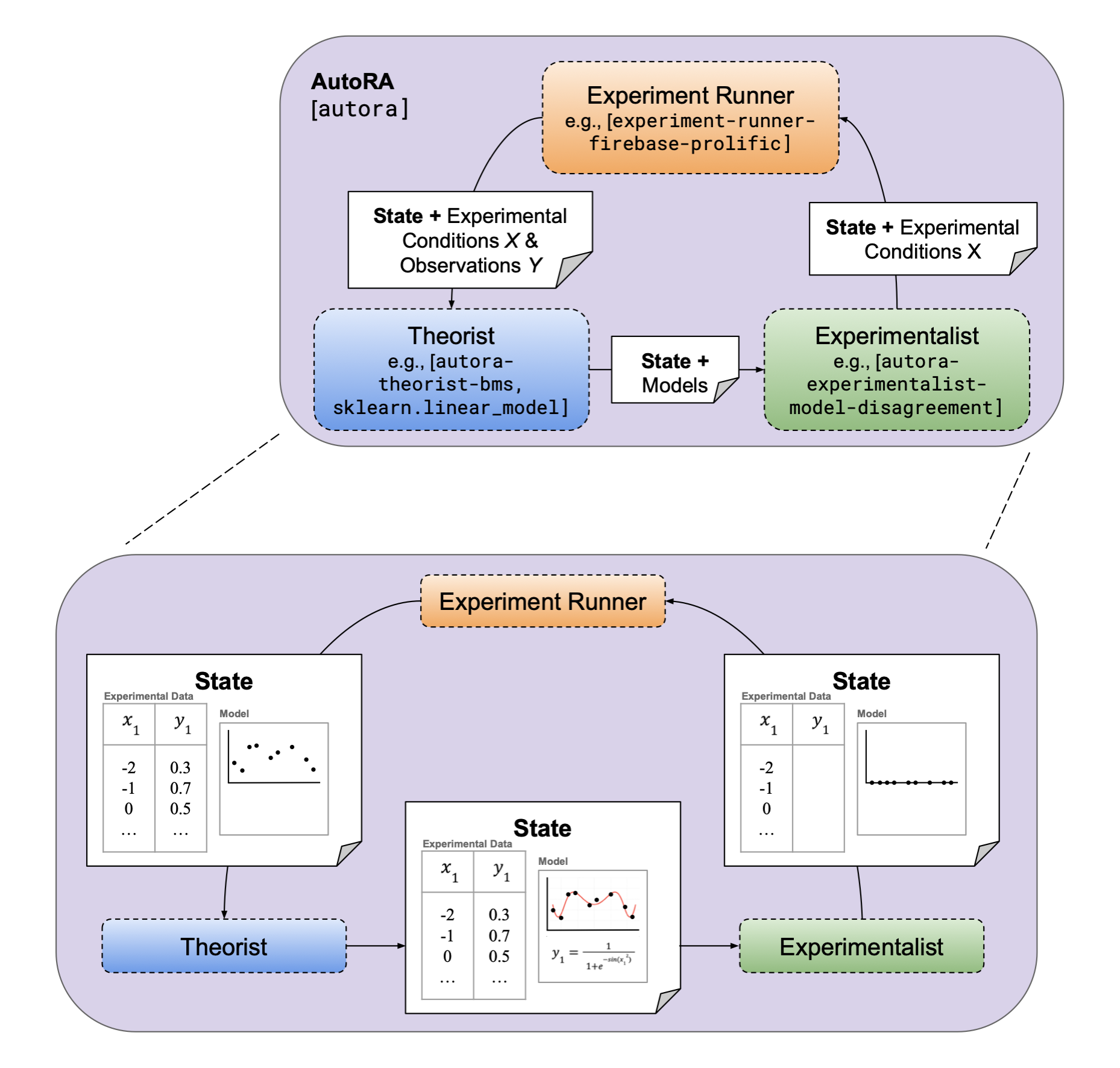
In tutorial I, we had experimentalists define new conditions, experiment runners collect new observations, and theorists model the data. To do this, we used the output of one as the input of the other, such as:

conditions = experimentalist(...) $\rightarrow$
observations = experiment_runner(conditions,...) $\rightarrow$
model = theorist(conditions, observations)

This chaining is embedded within the State functionality. To act on a state, we must wrap each of our experimentalist(s), experiment_runner(s), and theorist(s) so that they:

• operate on the State, and
• return a modified object of the same type State.

Defining The State¶

We use the StandardState object. Let's begin by populating the state with variable information (variables), seed condition data (conditions), and a dataframe (pd.DataFrame(columns=["x","y"])) that will hold our conditions (x) and observations (y).

Note: Some autora components have a random_state parameter that sets the seed for random number generators. Using this parameter ensures reproducibility of your code, but is optional.

In [ ]:

from autora.variable import Variable, ValueType, VariableCollection
from autora.experimentalist.random import random_pool
from autora.state import StandardState

#### Define variable data ####
iv = Variable(name="x", value_range=(0, 2 * np.pi), allowed_values=np.linspace(0, 2 * np.pi, 30))
dv = Variable(name="y", type=ValueType.REAL)
variables = VariableCollection(independent_variables=[iv],dependent_variables=[dv])

#### Define seed condition data ####
conditions = random_pool(variables, num_samples=10, random_state=0)

#### Initialize State ####
s = StandardState(
    variables = variables,
    conditions = conditions,
    experiment_data = pd.DataFrame(columns=["x","y"])
)

from autora.variable import Variable, ValueType, VariableCollection from autora.experimentalist.random import random_pool from autora.state import StandardState #### Define variable data #### iv = Variable(name="x", value_range=(0, 2 * np.pi), allowed_values=np.linspace(0, 2 * np.pi, 30)) dv = Variable(name="y", type=ValueType.REAL) variables = VariableCollection(independent_variables=[iv],dependent_variables=[dv]) #### Define seed condition data #### conditions = random_pool(variables, num_samples=10, random_state=0) #### Initialize State #### s = StandardState( variables = variables, conditions = conditions, experiment_data = pd.DataFrame(columns=["x","y"]) )

Viewing the State¶

Now, let's view the contents of the state we just initialized.

In [ ]:

print(s)

print(s)

StandardState(variables=VariableCollection(independent_variables=[Variable(name='x', value_range=(0, 6.283185307179586), allowed_values=array([0.        , 0.21666156, 0.43332312, 0.64998469, 0.86664625,
       1.08330781, 1.29996937, 1.51663094, 1.7332925 , 1.94995406,
       2.16661562, 2.38327719, 2.59993875, 2.81660031, 3.03326187,
       3.24992343, 3.466585  , 3.68324656, 3.89990812, 4.11656968,
       4.33323125, 4.54989281, 4.76655437, 4.98321593, 5.1998775 ,
       5.41653906, 5.63320062, 5.84986218, 6.06652374, 6.28318531]), units='', type=<ValueType.REAL: 'real'>, variable_label='', rescale=1, is_covariate=False)], dependent_variables=[Variable(name='y', value_range=None, allowed_values=None, units='', type=<ValueType.REAL: 'real'>, variable_label='', rescale=1, is_covariate=False)], covariates=[]), conditions=          x
0  5.416539
1  4.116570
2  3.249923
3  1.733292
4  1.949954
5  0.216662
6  0.433323
7  0.000000
8  1.083308
9  5.199877, experiment_data=Empty DataFrame
Columns: [x, y]
Index: [], models=[])

We can view all of the content we provided the state more directly if we choose.

In [ ]:

print("\033[1mThe variables we provided:\033[0m")
print(s.variables)

print("\n\033[1mThe conditions we provided:\033[0m")
print(s.conditions)

print("\n\033[1mThe dataframe we provided:\033[0m")
print(s.experiment_data)

print("\033[1mThe variables we provided:\033[0m") print(s.variables) print("\n\033[1mThe conditions we provided:\033[0m") print(s.conditions) print("\n\033[1mThe dataframe we provided:\033[0m") print(s.experiment_data)

The variables we provided:
VariableCollection(independent_variables=[Variable(name='x', value_range=(0, 6.283185307179586), allowed_values=array([0.        , 0.21666156, 0.43332312, 0.64998469, 0.86664625,
       1.08330781, 1.29996937, 1.51663094, 1.7332925 , 1.94995406,
       2.16661562, 2.38327719, 2.59993875, 2.81660031, 3.03326187,
       3.24992343, 3.466585  , 3.68324656, 3.89990812, 4.11656968,
       4.33323125, 4.54989281, 4.76655437, 4.98321593, 5.1998775 ,
       5.41653906, 5.63320062, 5.84986218, 6.06652374, 6.28318531]), units='', type=<ValueType.REAL: 'real'>, variable_label='', rescale=1, is_covariate=False)], dependent_variables=[Variable(name='y', value_range=None, allowed_values=None, units='', type=<ValueType.REAL: 'real'>, variable_label='', rescale=1, is_covariate=False)], covariates=[])

The conditions we provided:
          x
0  5.416539
1  4.116570
2  3.249923
3  1.733292
4  1.949954
5  0.216662
6  0.433323
7  0.000000
8  1.083308
9  5.199877

The dataframe we provided:
Empty DataFrame
Columns: [x, y]
Index: []

AutoRA Components and the State¶

Now that we have initialized the state, we need to start preparing components of autora to work with the state - namely, experimentalists, experiment runners, and theorists.

These components are defined in the same way as past tutorials. All we need to do so that these can function within the state is to wrap them in specialized state functions. Note that as the theorists are using the scikit-learn interface, this will need to be wrapped differently than the experiment runners and experimentalists. The wrappers are:

• on_state() for experiment runners and experimentalists
• estimator_on_state() for theorists (specifically, scikit-learn estimators)

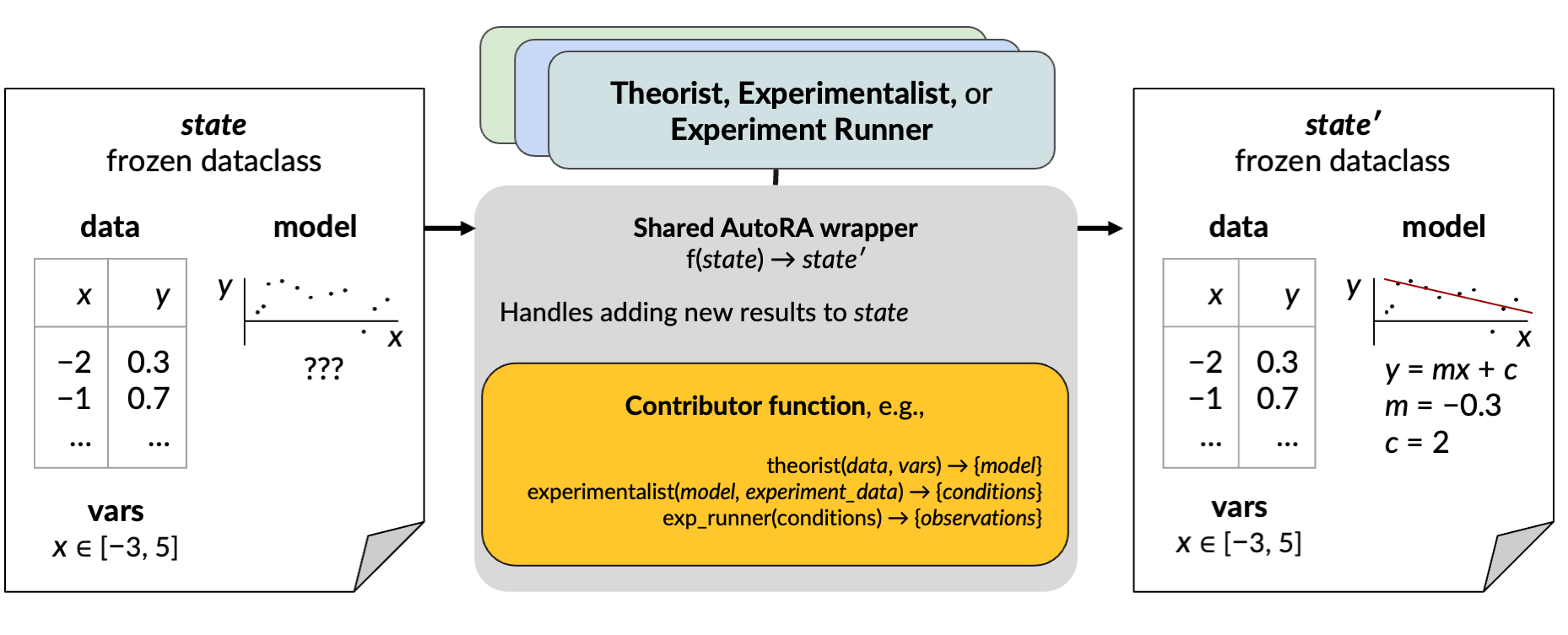
The first argument for each wrapper should be your corresponding function (i.e., the experiment runner, the experimentalist, and the theorist). The on_state wrapper takes a second argument, output, to determine where in the state the component is acting on. For the experimentalist this will be output=["conditions"], and for the experiment runner this will be output=["experiment_data"].

Once the components are wrapped, their functionality changes to act on the state, meaning that they now expect a state as the first input and will return a modified version of that state.

Wrapping Components to Work with State¶

Experimentalist Defined and Wrapped with State¶

We will use autora's random_pool pooler for our experimentalist. We import this and then wrap it so that it functions with the state.

In [ ]:

from autora.experimentalist.random import random_pool
from autora.state import on_state

experimentalist = on_state(random_pool, output=["conditions"])

from autora.experimentalist.random import random_pool from autora.state import on_state experimentalist = on_state(random_pool, output=["conditions"])

Experiment Runner Defined and Wrapped with State¶

We define a sine experiment runner and then wrap it so that it functions with the state.

To create our experiment runner, we will use an AutoRA function called equation_experiment(). This function takes in an equation wrapped as a sympy object using sp.simplify() and then allows us to solve for any input (x) given. Further, we constrain the values that this function can output by passing it the variable information.

In [ ]:

import sympy as sp
from autora.experiment_runner.synthetic.abstract.equation import equation_experiment
from autora.state import on_state

#### Define variable data ####
iv = Variable(name="x", value_range=(0, 2 * np.pi), allowed_values=np.linspace(0, 2 * np.pi, 30))
dv = Variable(name="y", type=ValueType.REAL)
variables = VariableCollection(independent_variables=[iv],dependent_variables=[dv])

#### Equation Experiment Method ####
sin_experiment = equation_experiment(sp.simplify('sin(x)'), variables.independent_variables, variables.dependent_variables[0])
sin_runner = sin_experiment.run

experiment_runner = on_state(sin_runner, output=["experiment_data"])

import sympy as sp from autora.experiment_runner.synthetic.abstract.equation import equation_experiment from autora.state import on_state #### Define variable data #### iv = Variable(name="x", value_range=(0, 2 * np.pi), allowed_values=np.linspace(0, 2 * np.pi, 30)) dv = Variable(name="y", type=ValueType.REAL) variables = VariableCollection(independent_variables=[iv],dependent_variables=[dv]) #### Equation Experiment Method #### sin_experiment = equation_experiment(sp.simplify('sin(x)'), variables.independent_variables, variables.dependent_variables[0]) sin_runner = sin_experiment.run experiment_runner = on_state(sin_runner, output=["experiment_data"])

Theorist Defined and Wrapped with State¶

We will use autora's BMSRegressor theorist. We import this and then wrap it so that if functions with the state.

In [ ]:

from autora.theorist.bms import BMSRegressor
from autora.state import estimator_on_state

theorist = estimator_on_state(BMSRegressor(epochs=100))

from autora.theorist.bms import BMSRegressor from autora.state import estimator_on_state theorist = estimator_on_state(BMSRegressor(epochs=100))

Running Each Component with the State¶

Run the Experimentalist¶

Let's run the experimentalist with the state and see how the state changes.

In [ ]:

print('\033[1mPrevious Conditions:\033[0m')
print(s.conditions)

s = experimentalist(s, num_samples=10, random_state=42)

print('\n\033[1mUpdated Conditions:\033[0m')
print(s.conditions)

print('\033[1mPrevious Conditions:\033[0m') print(s.conditions) s = experimentalist(s, num_samples=10, random_state=42) print('\n\033[1mUpdated Conditions:\033[0m') print(s.conditions)

Previous Conditions:
          x
0  5.416539
1  4.116570
2  3.249923
3  1.733292
4  1.949954
5  0.216662
6  0.433323
7  0.000000
8  1.083308
9  5.199877

Updated Conditions:
          x
0  0.433323
1  4.983216
2  4.116570
3  2.816600
4  2.599939
5  5.416539
6  0.433323
7  4.333231
8  1.299969
9  0.433323

Run the Experiment Runner¶

Let's run the experiment runner and see how the state changes.

In [ ]:

print("\033[1mPrevious Data:\033[0m")
print(s.experiment_data)

s = experiment_runner(s, added_noise=1.0, random_state=42)

print("\n\033[1mUpdated Data:\033[0m")
print(s.experiment_data)

print("\033[1mPrevious Data:\033[0m") print(s.experiment_data) s = experiment_runner(s, added_noise=1.0, random_state=42) print("\n\033[1mUpdated Data:\033[0m") print(s.experiment_data)

Previous Data:
Empty DataFrame
Columns: [x, y]
Index: []

Updated Data:
          x         y
0  0.433323  0.724606
1  4.983216 -2.003534
2  4.116570 -0.077238
3  2.816600  1.259866
4  2.599939 -1.435481
5  5.416539 -2.064342
6  0.433323  0.547730
7  4.333231 -1.245219
8  1.299969  0.946749
9  0.433323 -0.433155

Run the Theorist¶

Let's run the theorist and see how the state changes. Note that theorists should return a single model directly or multiple models within a list to work with the state.

In [ ]:

s = theorist(s)

print("\n\033[1mUpdated Model:\033[0m")
print(s.models[-1])

plot_from_state(s,'sin(x)')

s = theorist(s) print("\n\033[1mUpdated Model:\033[0m") print(s.models[-1]) plot_from_state(s,'sin(x)')

INFO:autora.theorist.bms.regressor:BMS fitting started
100%|██████████| 100/100 [00:04<00:00, 23.00it/s]
INFO:autora.theorist.bms.regressor:BMS fitting finished

Updated Model:
-0.38

Component Chaining¶

As such, we have our autora components wrapped to work with the state. Remember, this means that they take the state as an input and returns the updated state as an output. As the components all act on the state, they can easily be chained.

In [ ]:

s = experimentalist(s, num_samples=10, random_state=42)
s = experiment_runner(s, added_noise=1.0, random_state=42)
s = theorist(s)

print(s)
plot_from_state(s,'sin(x)')

s = experimentalist(s, num_samples=10, random_state=42) s = experiment_runner(s, added_noise=1.0, random_state=42) s = theorist(s) print(s) plot_from_state(s,'sin(x)')

INFO:autora.theorist.bms.regressor:BMS fitting started
100%|██████████| 100/100 [00:04<00:00, 20.52it/s]
INFO:autora.theorist.bms.regressor:BMS fitting finished

StandardState(variables=VariableCollection(independent_variables=[Variable(name='x', value_range=(0, 6.283185307179586), allowed_values=array([0.        , 0.21666156, 0.43332312, 0.64998469, 0.86664625,
       1.08330781, 1.29996937, 1.51663094, 1.7332925 , 1.94995406,
       2.16661562, 2.38327719, 2.59993875, 2.81660031, 3.03326187,
       3.24992343, 3.466585  , 3.68324656, 3.89990812, 4.11656968,
       4.33323125, 4.54989281, 4.76655437, 4.98321593, 5.1998775 ,
       5.41653906, 5.63320062, 5.84986218, 6.06652374, 6.28318531]), units='', type=<ValueType.REAL: 'real'>, variable_label='', rescale=1, is_covariate=False)], dependent_variables=[Variable(name='y', value_range=None, allowed_values=None, units='', type=<ValueType.REAL: 'real'>, variable_label='', rescale=1, is_covariate=False)], covariates=[]), conditions=          x
0  0.433323
1  4.983216
2  4.116570
3  2.816600
4  2.599939
5  5.416539
6  0.433323
7  4.333231
8  1.299969
9  0.433323, experiment_data=           x         y
0   0.433323  0.724606
1   4.983216 -2.003534
2   4.116570 -0.077238
3   2.816600  1.259866
4   2.599939 -1.435481
5   5.416539 -2.064342
6   0.433323  0.547730
7   4.333231 -1.245219
8   1.299969  0.946749
9   0.433323 -0.433155
10  0.433323  0.724606
11  4.983216 -2.003534
12  4.116570 -0.077238
13  2.816600  1.259866
14  2.599939 -1.435481
15  5.416539 -2.064342
16  0.433323  0.547730
17  4.333231 -1.245219
18  1.299969  0.946749
19  0.433323 -0.433155, models=[-0.38, -0.38])

The Cycle¶

Moreover, we can use these chained components within a loop to run multiple cycles.

Cycle using Number of Cycles¶

In [ ]:

#### First, let's reinitialize the state object to get a clean state ####
iv = Variable(name="x", value_range=(0, 2 * np.pi), allowed_values=np.linspace(0, 2 * np.pi, 30))
dv = Variable(name="y", type=ValueType.REAL)
variables = VariableCollection(independent_variables=[iv],dependent_variables=[dv])

conditions = random_pool(variables, num_samples=10, random_state=42)

s = StandardState(
    variables = variables,
    conditions = conditions,
    experiment_data = pd.DataFrame(columns=["x","y"])
)

### Then we cycle through the pipeline we built three more times ###
num_cycles = 3 # number of empirical research cycles
for cycle in range(num_cycles):
    #Run pipeline
    s = experimentalist(s, num_samples=10, random_state=42+cycle)
    s = experiment_runner(s, added_noise=1.0, random_state=42+cycle)
    s = theorist(s)
    
    #Report metrics
    print(f"\n\033[1mRunning Cycle {cycle+1}:\033[0m")
    print(f"\033[1mCycle {cycle+1} model: {s.models[-1]}\033[0m")
    plot_from_state(s,'sin(x)')

#### First, let's reinitialize the state object to get a clean state #### iv = Variable(name="x", value_range=(0, 2 * np.pi), allowed_values=np.linspace(0, 2 * np.pi, 30)) dv = Variable(name="y", type=ValueType.REAL) variables = VariableCollection(independent_variables=[iv],dependent_variables=[dv]) conditions = random_pool(variables, num_samples=10, random_state=42) s = StandardState( variables = variables, conditions = conditions, experiment_data = pd.DataFrame(columns=["x","y"]) ) ### Then we cycle through the pipeline we built three more times ### num_cycles = 3 # number of empirical research cycles for cycle in range(num_cycles): #Run pipeline s = experimentalist(s, num_samples=10, random_state=42+cycle) s = experiment_runner(s, added_noise=1.0, random_state=42+cycle) s = theorist(s) #Report metrics print(f"\n\033[1mRunning Cycle {cycle+1}:\033[0m") print(f"\033[1mCycle {cycle+1} model: {s.models[-1]}\033[0m") plot_from_state(s,'sin(x)')

INFO:autora.theorist.bms.regressor:BMS fitting started
100%|██████████| 100/100 [00:04<00:00, 22.28it/s]
INFO:autora.theorist.bms.regressor:BMS fitting finished

Running Cycle 1:
Cycle 1 model: -0.38

INFO:autora.theorist.bms.regressor:BMS fitting started
100%|██████████| 100/100 [00:05<00:00, 18.47it/s]
INFO:autora.theorist.bms.regressor:BMS fitting finished

Running Cycle 2:
Cycle 2 model: -0.27

INFO:autora.theorist.bms.regressor:BMS fitting started
100%|██████████| 100/100 [00:04<00:00, 21.55it/s]
INFO:autora.theorist.bms.regressor:BMS fitting finished

Running Cycle 3:
Cycle 3 model: sin(x)

Cycle using Stopping Criteria¶

Alternatively, we can run the chain until we reach a stopping criterion. For example, here we will loop until we get 40 datapoints.

In [ ]:

#### First, let's reinitialize the state object to get a clean state ####
iv = Variable(name="x", value_range=(0, 2 * np.pi), allowed_values=np.linspace(0, 2 * np.pi, 30))
dv = Variable(name="y", type=ValueType.REAL)
variables = VariableCollection(independent_variables=[iv],dependent_variables=[dv])

conditions = random_pool(variables, num_samples=10, random_state=42)

s = StandardState(
    variables = variables,
    conditions = conditions,
    experiment_data = pd.DataFrame(columns=["x","y"])
)

### Then we cycle through the pipeline we built until we reach our stopping criterion ###
cycle = 0
while len(s.experiment_data) < 40: #Run until we have at least 40 datapoints
    #Run pipeline
    s = experimentalist(s, num_samples=10, random_state=42+cycle)
    s = experiment_runner(s, added_noise=1.0, random_state=42+cycle)
    s = theorist(s)
    
    #Report metrics
    print(f"\n\033[1mRunning Cycle {cycle+1}, number of datapoints: {len(s.experiment_data)}\033[0m")
    print(f"\033[1mCycle {cycle+1} model: {s.models[-1]}\033[0m")
    plot_from_state(s,'sin(x)')
    
    #Increase count
    cycle += 1

print(f"\n\033[1mNumber of datapoints: {len(s.experiment_data)}\033[0m")
print(f"\033[1mDetermined Model: {s.models[-1]}\033[0m")

#### First, let's reinitialize the state object to get a clean state #### iv = Variable(name="x", value_range=(0, 2 * np.pi), allowed_values=np.linspace(0, 2 * np.pi, 30)) dv = Variable(name="y", type=ValueType.REAL) variables = VariableCollection(independent_variables=[iv],dependent_variables=[dv]) conditions = random_pool(variables, num_samples=10, random_state=42) s = StandardState( variables = variables, conditions = conditions, experiment_data = pd.DataFrame(columns=["x","y"]) ) ### Then we cycle through the pipeline we built until we reach our stopping criterion ### cycle = 0 while len(s.experiment_data) < 40: #Run until we have at least 40 datapoints #Run pipeline s = experimentalist(s, num_samples=10, random_state=42+cycle) s = experiment_runner(s, added_noise=1.0, random_state=42+cycle) s = theorist(s) #Report metrics print(f"\n\033[1mRunning Cycle {cycle+1}, number of datapoints: {len(s.experiment_data)}\033[0m") print(f"\033[1mCycle {cycle+1} model: {s.models[-1]}\033[0m") plot_from_state(s,'sin(x)') #Increase count cycle += 1 print(f"\n\033[1mNumber of datapoints: {len(s.experiment_data)}\033[0m") print(f"\033[1mDetermined Model: {s.models[-1]}\033[0m")

INFO:autora.theorist.bms.regressor:BMS fitting started
100%|██████████| 100/100 [00:04<00:00, 23.04it/s]
INFO:autora.theorist.bms.regressor:BMS fitting finished

Running Cycle 1, number of datapoints: 10
Cycle 1 model: -0.38

INFO:autora.theorist.bms.regressor:BMS fitting started
100%|██████████| 100/100 [00:05<00:00, 19.61it/s]
INFO:autora.theorist.bms.regressor:BMS fitting finished

Running Cycle 2, number of datapoints: 20
Cycle 2 model: -0.27

INFO:autora.theorist.bms.regressor:BMS fitting started
100%|██████████| 100/100 [00:04<00:00, 22.35it/s]
INFO:autora.theorist.bms.regressor:BMS fitting finished

Running Cycle 3, number of datapoints: 30
Cycle 3 model: -0.07

INFO:autora.theorist.bms.regressor:BMS fitting started
100%|██████████| 100/100 [00:04<00:00, 21.30it/s]
INFO:autora.theorist.bms.regressor:BMS fitting finished

Running Cycle 4, number of datapoints: 40
Cycle 4 model: sin(x)