Experimentalist Overview

The primary goal of an experimentalist is to identify experiments that yield scientific merit. autora implements techniques for automating the identification of novel experiments.

An experiment consists of a series of conditions \(\vec{x} \in X\). The variables manipulated in each condition are defined as independent variables. As an example, consider a visual discrimination task in which participants are presented with two lines of different lengths, and are asked to indicate which line is longer. There are two independent variables in this experiment: the length of the first line and the length of the second line, which each have values (e.g., 2.0 cm for the first line and 2.1 cm for the second line). Thus, a condition is a vector of values that corresponds to a specific combination of values of the independent variables \(x_i\).

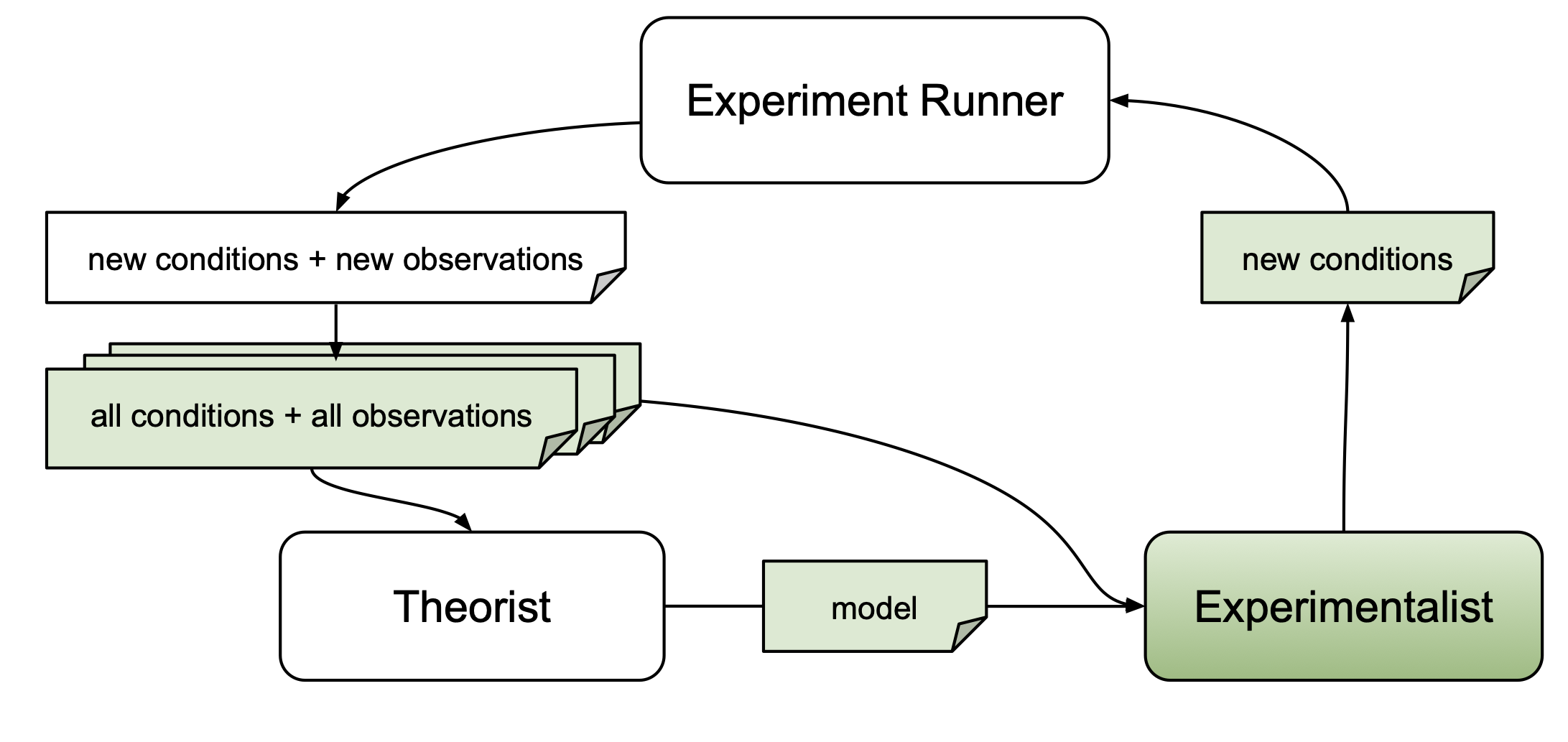
Experimentalists may use information about candidate models \(M\) obtained from a theorist, conditions that have already been probed \(\vec{x}' \in X'\), or respective observations \(\vec{y}' \in Y'\). The following table includes the experimentalists currently implemented in autora.

Name	Links	Description	Arguments
Random	Package, Docs	An experimentalist with pooling and sampling functionality. The pooler creates combinations of conditions from lists of discrete values using random selection; the sampler draws from a pool of conditions without replacement using uniform random sampling.
Novelty	Package, Docs	Identifies conditions \(\vec{x}' \in X'\) with respect to a pairwise distance metric applied to existing conditions \(\vec{x} \in X\).	\(X'\)
Uncertainty	Package, Docs	Identifies conditions \(\vec{x}' \in X'\) with respect to model uncertainty, which can be calculated in three different ways.	\(M\)
Model Disagreement	Package, Docs	Identifies conditions \(\vec{x}' \in X'\) with respect to a pairwise distance metric between theorist models, \(P_{M_{i}}(\hat{y}, \vec{x}')\).	\(M\)
Falsification	Package, Docs	An experimentalist with pooling and sampling functionality that generates and samples from novel conditions under which the loss \(\hat{\mathcal{L}}(M,X,Y,X')\) of the best candidate model is predicted to be the highest.	\(M, X', Y'\)
Mixture	Package, Docs	Uses a mixture of specified sampling strategies to identify novel conditions. Conditions are selected based on a weighted sum of scores obtained from the specified strategies.	\(M, X', Y'\)
Nearest Value	Package, Docs	Returns the nearest values between the input samples and the allowed values, without replacement.	\(X'\)
Leverage	Package, Docs	Identifies conditions using the statistical concept of leverage to refit candidate models iteratively with the leave-one-out method.	\(M, X', Y'\)
Inequality	Package, Docs	Uses a pairwise distance metric to compare and select new conditions. This metric along with a difference threshold are used to calculate inequality scores for candidate conditions, and conditions with the highest scores are chosen.	\(X'\)